Penúltimo capítulo del curso de combinatoria. Tengo bautizado como simplificar a la generación de combinaciones que tengan un mínimo fijo de signos distintos entre sus columnas.
Es un concepto tan general que abarca todo el universo de los 14 triples, un grupo de columnas, el que sea, es una simplificada a distancia N si todas sus columnas tienen como mínimo N signos distintos con cualquier pareja que se tome.
Es independiente de poner fijos, dobles o cualquier tipo de condición y es compatible con todas.
Las simplificadas tienen la propiedad de que a una distancia determinada abarcan el máximo posible de cobertura y el mínimo de solapamiento, eso maximiza la probabilidad de acierto, no tiene más secreto.
Como cualquier columna que se tome tiene siempre la misma cobertura, porque no dependen de las columnas, con las simplificadas se gana en regularidad de acierto porque se minimiza el solapamiento, se acierta con más frecuencia pero cuando se acierta se tienen menos columnas con premio, más frecuencia, menos cantidad de aciertos cuando se acierta.
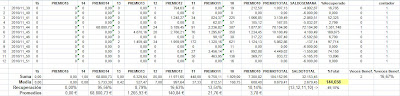
Estoy publicando las tablas de récords de todas las combinaciones de triples y dobles a una distancia determinada, estas combinaciones son las que tienen más columnas a esa distancia dentro de cada sesarrollo.
Se busca que sea la que tenga más columnas para que haya el máximo posible de columnas cubiertas evitando solapamientos, es un concepto distinto del de reducir, las simplificadas no buscan la cobertura total del desarrollo con el mínimo de columnas, buscan la cobertura máxima y solapamiento mínimo con el máximo de columnas.
Mi ejemplo favorito de combinación simplificada son los 13 triples a distancia 9, combinatoriamente hablando es perfecta, estas 27 columnas:
11111111111111XXXXXXXXX1111122222222211111222XXX111XXX11111222XXXXXX11XXX111222XXX11XXX22211122211222111XXX22211111XXX222222112X12X12X12X1X112X12X12X2X1X1X12X12X122X1X1X1212X2X112XX12X1X1212X12XX112X2X1X1212XX112XX122X1X12X1X122X112XX12X12X112XX12X12X1X21X21X21X212121X21X21XX21211X21X21X2X21211X221XX2121X21X211X221X21X2121XX211X221X2121X1X2X211X2211X2X2121X1X221X2121X1X21X221 Son la perfección absoluta, son 27 columnas en las que cualquier pareja que se tome tiene exactamente 9 signos distintos entre ellas, por ejemplo, como está la todo “1”, todas las demás tienen exactamente 5 “1” (9 variantes).
Cualquier pareja de columnas que se tome con 9 signos distintos es una reducida de 9 dobles al 10, como tenemos 27 columnas, se pueden formar
(27 * 26) / 2 = 351 parejas distintas.
Esta combinación de 27 columnas encierra 351 reducidas de 9 dobles al 10.
Como todas las columnas tienen 9 signos distintos entre ellas es imposible tener 2 columnas con 10 aciertos porque tendrían 8 signos distintos, estas 27 columnas garantizan una y solo una columna premiada.
Máxima cobertura, no se puede abarcar más con 27 columnas.
Mínimo solapamiento, tan mínimo que es nulo al 10.
Se ha fallado el R.Madrid y el Barça porque tenían la "X" (era mas rentable) y fallos rentables en Villarreal, Betis, Espanyol...
